前言
- 这篇博客的初心 : 最近读的论文又用到LSTM了,发现对这些深度学习模型我还是只了解皮毛(前向传播),不了解其底层原理(如参数的更新),而我从接触深度学习开始就对反向传播充满了好奇,感觉这是个很难理解的事情。所以建立这篇博客慢慢从矩阵求导开始,慢慢推导所有深度学习模型的底层原理,从而加深自己的理解。
- 这篇博客内容 : 包括部分深度学习所需数学知识,以及各种深度学习模型(DNN,RNN等)的原理推导。
1 数学知识
注: 在本博客中,所有向量$\bm{v}$默认都为列向量
1.1 深度学习中几种常见的梯度计算
在神经网络中,很常见的求梯度类型求一个向量$\bm{v}$(如网络某一层的输出)或一个矩阵$\bm{W}$(如网络中的参数)的梯度,他们的实质其实都是多元函数求偏导。其中这个多元函数$f$(如损失函数)是以$\bm{v}$或者$\bm{W}$为自变量的实值函数。
1.1.1 求向量的梯度
\[若\bm{v}=\begin{pmatrix} v_1 \\ v_2 \\ ... \\v_n \end{pmatrix},则\frac{\partial f}{\partial \bm{v}}=\begin{pmatrix} \frac{\partial f}{\partial v_1} \\ \frac{\partial f}{\partial v_2} \\ ... \\\frac{\partial f}{\partial v_n} \end{pmatrix}\]1.1.2 求矩阵的梯度
同1.1.1,即使用$f$依次对矩阵的每一个元素求偏导,最后的结果仍然为一个矩阵。
2 深度神经网络(DNN)中反向传播的推导
由于网络上很多教程都是标量直接对向量或矩阵求导,非常难以理解。而一种很好的方式就是先对向量或矩阵的最小单元(元素) 求导,然后泛化到整个向量或矩阵。这在cs231n中也有提到:
Work with small, explicit examples. Some people may find it difficult at first to derive the gradient updates for some vectorized expressions. Our recommendation is to explicitly write out a minimal vectorized example, derive the gradient on paper and then generalize the pattern to its efficient, vectorized form
所以我整篇文章都是只考虑对最小单元求导,这对于整个算法的深刻理解是有很大帮助的。
2.1 变量定义
| 符号 | 含义 |
|---|---|
| $N_l$ | 第$l$层神经元数量 |
| $\bm{x}$ | 一个输入样本,维度为($N_0\times 1$) |
| $\bm{y}$ | 这个输入样本的标签,维度为($N_L\times 1$) |
| $W_{jk}^l$ | 第$l-1$层第$\bm{k}$个神经元到第$l$层第$\bm{j}$个神经元的连接权重 |
| $b_j^l$ | 第$l$层第$j$个神经元的偏置 |
| $z_j^l$ | 第$l$层第$j$个神经元的带权输入 |
| $\sigma^l$ | 第$l$层的激活函数 |
| $a_j^l$ | 第$l$层第$j$个神经元的输出 |
2.2 前向传播
为方便考虑传播过程,我们首先仅考虑一个样本$\bm{x}$在DNN中的前向传播。
很容易发现,样本在每一层中流动的过程都是一样的,可以表示为:
\[\begin{aligned} &\bm{z^l}=\bm{W^la^{l-1}+b^l}\\ &\bm{a^l}=\sigma^l(\bm{z^l}) \end{aligned}\]其中,$\bm{a^0}=\bm{x}$,$\bm{W^l}$的维度为$(N_{l}\times N_{l-1})$,$\bm{a^{l-1}}$的维度为$(N_{l-1}\times1)$,$\bm{b^l,z^l,a^l}$的维度均为$(N_l\times1)$,$\bm{a^L}$是DNN的输出
通过前向传播,样本$\bm{x}$一层一层地通过DNN走到了输出层,并得到了$\bm{a^L}$。那么我们就能够通过$\bm{a^L}$和真实的标签$\bm{y}$得到这个样本的损失,即$C=Loss(\bm{a^L,y})$。
2.3 接下来要做的事情
我们希望根据这个损失$C$来不断的更新DNN的参数$[\bm{W^1,W^2,…,W^L}及\bm{b^1,b^2,…,b^l}]$。为了使用基于梯度的优化算法,很显然需要计算所有参数的梯度,也就是$[\frac{\partial C}{\partial\bm{W^1}},\frac{\partial C}{\partial\bm{W^2}},…,\frac{\partial C}{\partial\bm{W^L}}]$及$[\frac{\partial C}{\partial\bm{b^1}},\frac{\partial C}{\partial\bm{b^2}},…,\frac{\partial C}{\partial\bm{b^L}}]$。
由1.1.1和1.1.2可知,求向量或矩阵的梯度,就是对其中的每一个元素分别求偏导,所以我们开始吧。
2.3.1 求$\bm{W^l}$的梯度
我们只考虑第$l$层参数矩阵$\bm{W^l}$中的一个元素$W_{jk}^l$的梯度,来看看有什么规律。
$W_{jk}^l$会对$C$有什么影响呢?他只会与第$l-1$层第$\bm{k}$个节点的输出$a_k^{l-1}$相乘,然后作为一部分汇聚到下一层,也就是第$l$层的第$\bm{j}$个节点上。如图所示:
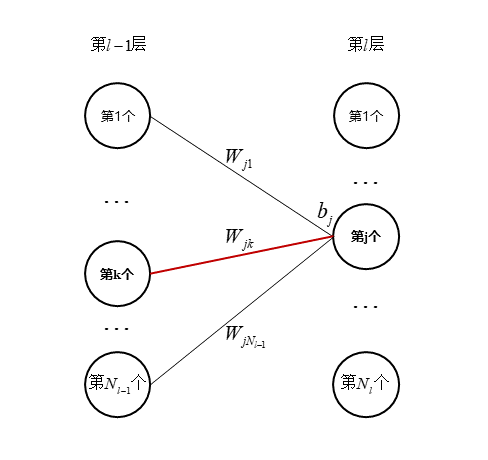
所以根据链式法则,有$\frac{\partial C}{\partial W_{jk}^l}=\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial W_{jk}^l}$。其中,$z_j^l=\sum_{i=1}^{N_{l-1}}a_i^{l-1}W_{ji}^l+b_j^l$
所以,$\frac{\partial z_j^l}{\partial W_{jk}^l}=a_k^{l-1}$(仅当$i=k$时,求和项不为0), 从而:
\[\frac{\partial C}{\partial W_{jk}^l}=\frac{\partial C}{\partial z_j^l}a_k^{l-1}\]
2.3.2 求$\bm{b^l}$的梯度
同样,我们只考虑$b_j^l$的梯度。
$b_j^l$会对$C$有什么影响呢?他只会作用在第$l$层的第$\bm{j}$个节点上,作为一个小小的偏置(如上图)。所以我们依然可以根据链式法则得到$\frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial b_j^l}$。其中,$z_j^l=\sum_{i=1}^{N_{l-1}}a_i^{l-1}W_{ji}^l+b_j^l$(与2.3.1中是一样的)
所以,$\frac{\partial z_j^l}{\partial b_j^l}=1$,从而:
\[\frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\times1=\frac{\partial C}{\partial z_j^l}\]
2.4 (误差的)反向传播
通过2.3节可以看到:如果想求$\bm{W^l}$和$\bm{b^l}$中每一个元素的梯度,都需要求$\frac{\partial C}{\partial z_j^l}$这一项。该怎么求呢?接下来就是反向传播的精髓了。
我小小的总结一下,前向传播是训练样本的前向传播,目的是使用$\bm{x}$通过DNN得到$\bm{a^L}$,从而计算$Loss(\bm{a^L,y})$。那么反向传播是误差的反向传播,即首先根据$Loss$得到最后一层(第$L$层)的误差,再反向计算每一层的误差。这里的误差,也就是我们刚刚注意到的$\frac{\partial C}{\partial \bm{z^l}}$这一项。通过计算该项,我们便可以得到模型中所有参数的梯度,从而使用基于梯度的优化算法进行参数更新,这就是DNN完整的一轮迭代。
2.4.1 计算第$L$层的误差$\frac{\partial C}{\partial\bm{z^L}}$
同样的方法,我们还是先只考虑这一层中第$\bm{j}$个神经元的误差$\frac{\partial C}{\partial z_j^L}$。
首先考虑$z_j^L$会对$C$产生什么影响。很简单的,$z_j^L$在被激活函数$\sigma^L$激活得到$a_j^L$然后作为计算$C$的一部分。
所以,又根据链式法则,得到$\frac{\partial C}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L}$.
其中$\frac{\partial a_j^L}{\partial z_j^L}$这一项等于$\sigma’^L(z_j^L)$.因为$a_j^L=\sigma^L(z_j^L)$
而$\frac{\partial C}{\partial a_j^L}$这一项需要根据具体的损失函数$Loss()$来计算。我们以平方损失为例:
\[C=Loss(\bm{a^L,y})=\frac{1}{2}\Vert\bm{y-a^L}\Vert^2=\frac{1}{2}\sum_j(y_j-a_j^L)^2\]那么,我们便可以求得
\[\begin{aligned} \frac{\partial C}{\partial a_j^L}&=\partial \frac{1}{2}[(y_1-a_1^L)^2+...+(y_{N_L}-a_{N_L}^L)^2]/\partial a_j^L\\ &=\frac{1}{2}\times2(y_j-a_j^L)\times-1=a_j^L-y_j \end{aligned}\]可以看到$\frac{\partial C}{\partial a_j^L}和\frac{\partial a_j^L}{\partial z_j^L}$都是只与下标$\bm{j}$有关的,所以我们可以直接将其扩展成向量形式,即$\frac{\partial C}{\partial\bm{z^L}}=(\bm{a^L-y})\odot\sigma’^L(\bm{z^L})$,其中$\odot$是两个向量的按元素乘法
从平方损失函数扩展到其他各种损失函数,即
\[\frac{\partial C}{\partial\bm{z^L}}=(\frac{\partial C}{\partial \bm{a^L}})\odot\sigma'^L(\bm{z^L})\]
2.4.1 误差从第$l+1$层传播到第$l$层
为了计算误差在两层之间是怎么流动的,我们首先需要观察一下两层之间$\bm{z}$的关系,很简单,就是$\bm{z^{l+1}}=\bm{W^{l+1}}\sigma^l(\bm{z^l})+\bm{b^{l+1}}$
我们可以从上面的式子观察一下第$l$层的第$\bm{j}$个神经元的$z_j^l$是怎么作用到下一层的。同样很简单,$z_j^l$会先经过一个激活函数$\sigma$得到$a_j^l$,再乘上不同的权重,作用在下一层的每一个神经元上。
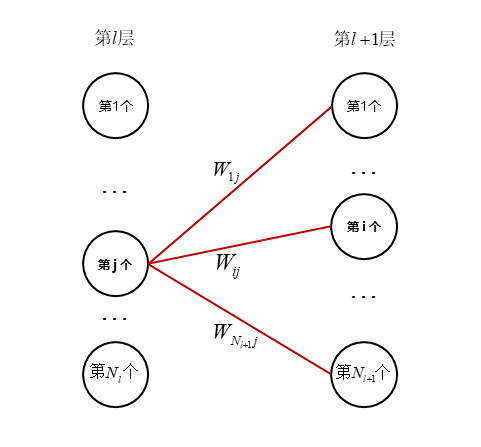
所以,根据链式法则(例:z为u,v的函数,u和v分别为x,y的函数),有$\frac{\partial C}{\partial z_j^l}=\sum_k\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}$
我们先看$\frac{\partial z_k^{l+1}}{\partial z_j^l}$这一项。$z_k^{l+1}$是怎么得到的呢?是上一层所有的$z_i^l$经过一个激活函数,再乘一个权重,最后加上一个偏置得到的,即$z_k^{l+1}=\sum_{i=1}^{N_l}\sigma^l(z_i^l)\times W_{ki}^{l+1}+b_k^{l+1}$.(形式同2.3.1图)
所以$\frac{\partial z_k^{l+1}}{\partial z_j^l}=\sigma’^l(z_j^l)\times W_{kj}^{l+1}$(仅当$i=j$时求和项不为0)
把他带回$\frac{\partial C}{\partial z_j^l}$,得到$\frac{\partial C}{\partial z_j^l}=\sum_k\frac{\partial C}{\partial z_k^{l+1}}\times W_{kj}^{l+1}\times\sigma’^l(z_j^l)$。
可以发现,上式$=[\bm{(W^{l+1})}^\mathrm{T}(\frac{\partial C}{\partial \bm{z^{l+1}}})]_j\times \sigma’^l(z_j^l)$
因为只由下标$\bm{j}$决定,所以又可以得到一个完美漂亮的向量表达~
\[\frac{\partial C}{\bm{\partial \bm{z^l}}}=\bm{(W^{l+1})}^\mathrm{T}(\frac{\partial C}{\partial \bm{z^{l+1}}})\odot\sigma'^l(\bm{z^l})\]
2.5 关于单样本反向传播的最后公式
为便于简洁表示,令每层的误差$\frac{\partial C}{\partial \bm{z^l}}=\bm{\delta^l}$
有以下公式:
\[\begin{aligned} &\frac{\partial C}{\partial W_{jk}^l}=\delta_j^la_k^{l-1}\\ &\frac{\partial C}{\partial b_j^l}=\delta_j^l\\ &\bm{\delta^L}=(\frac{\partial C}{\partial \bm{a^L}})\odot\sigma'^L(\bm{z^L})\\ &\bm{\delta^l}=(\bm{(W^{l+1})}^\mathrm{T}\bm{\delta^{l+1}})\odot\sigma'^l(\bm{z^l}) \end{aligned}\]
也可以按照以下流程编程实现(图片来自Neural Networks and Deep Learning, Michael Nielsen ):
 自此,我对于单个样本$\bm{x}$的反向传播推导就告一段落,已经可以凭借以上内容,实现一个使用随机梯度下降算法来优化的DNN啦!
自此,我对于单个样本$\bm{x}$的反向传播推导就告一段落,已经可以凭借以上内容,实现一个使用随机梯度下降算法来优化的DNN啦!
2.6 多样本反向传播
已更新:Full Matrix Method of mini-batch Back Propagation in DNN, hannlp
2.7 RNN的反向传播
已更新:Backward Propogation Through Time (BPTT) in RNN, hannlp